Testing the Program.
Testing and Optimizing the program.

Testing the program
After the program was complete, a series of testing methods were done to assure
that the code is correct. The following were tests done on the program:
- Variable and constants test. All the variables and constants were checked
to make sure that they have proper values throughout the program.
- Integration check. The Simson's integration subroutine was checked by using it
to integrate simple shapes and compared to that calculated by hand.
- Energy Calculation check. The subroutine used to calculate the potential
energy between the two configurations were tested and compared to that obtained from
hand calculation.
- CM check. The subroutine for calculating the center of mass of a group was
tested and compared.
- Movement and Rotation Check. To check whether the program is performing the proper rotation
around the chosen axis, and to see if new location after a rotation is correct, I used
Excel to help with the hand calculations. First, I obtained the two sets of random
numbers generated by the program. One set represents the axis of rotaion, and the other
represents the amount theta in which to rotate about. After knowing the initial
positions, the axis to rotate about, and the amount to rotate about, I used Excel to
calculate the positions of each beads after each rotation and compared them to those
obtained from the program. The values matched perfectly and I assumed that the code does
it correctly.
- Overall calculation Check. Appendix 8 Table A8.3 of "Intermolecular Forces -
Their origin and determination" by G.C. Maitland et. al.. Clarendon Press Oxford
1981, shows classical second virial coefficients for the
diatomic 12-6 potential. The second virial coefficients given are in reduced form.
It is a table that shows the reduced virial coefficients (B*=(2*pi/3)N
A*sigma3) versus the reduced temperature (T*=kB
T/Epsilon) at different reduced distances (R*=R/sigma) where R is the
bond length.
I tried running the program for different T* and R*
and calculate the B*s. After plotting the results with the documented values,
I obtained the following graph.
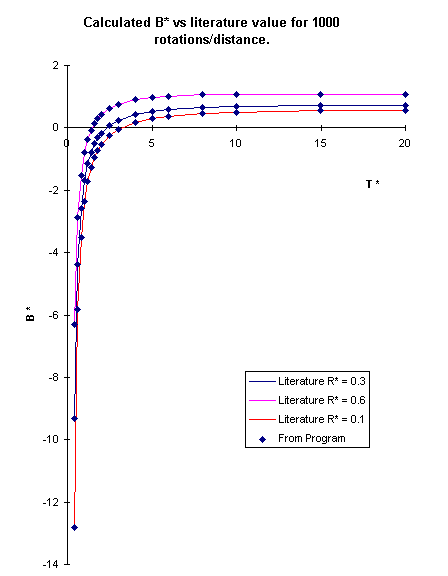
The lines are the values from the Appendix. The points were obtained from the
program. For each data point, the molecules rotate for 1000 times before changing
distances. It could be seen that the values almost perfectly match those from the
literature.
Optimizing the program
Most of the computational time was spent on rotating and moving the molecules.
A setting of 100,000 rotations per separation distance could take up to 3 or 4 hours
on the SP. To get a rough idea how the second virial coefficient changes with
changing distances and the number of rotations, I ran two test. The first test
was to change the maximum separation distance and keep the number of rotations constant.
The values of B2 were then compared and the difference between current and previous
values were plotted.
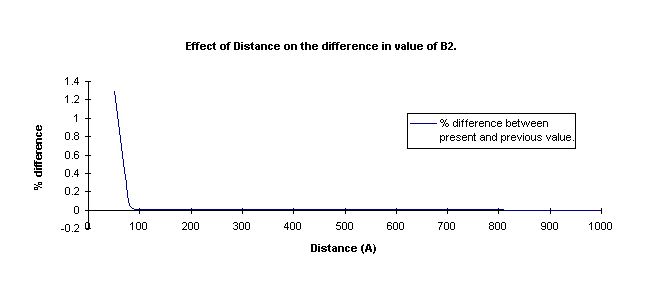
It is seen that the % difference changes very rapidly with increasing
maximum separation distance. The difference between B2 values at a maximum separation
distance of 100 A and 500 A is about 0.01 percent, and the b2 values at 500 A and
100 A are virtually identical (less than 0.0001 %). As a result, a maximum distance
of 500 A was used in the calculations.
The second test was keeping the maximum separation distance constant and
alter the number of rotations per distance. After applying various rotation trials,
a similar plot was obtained.
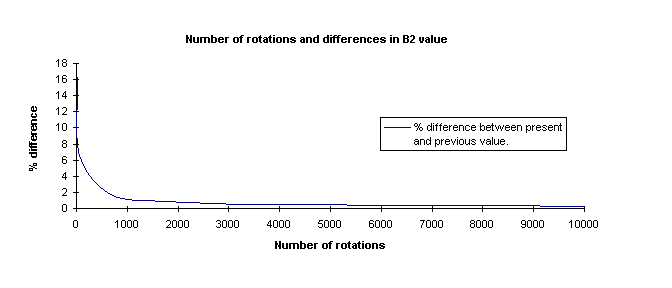
The difference rapidly decreases in the beginning but levels out gradually.
A trend line was fitted to the curve in order to obtain an equation which at least
represents the gradually falling trend. It could then be used to calculate the
number of rotations required to reach a certain amount of accuracy.
Using the function trendline on Excel, I obtained the following plots.
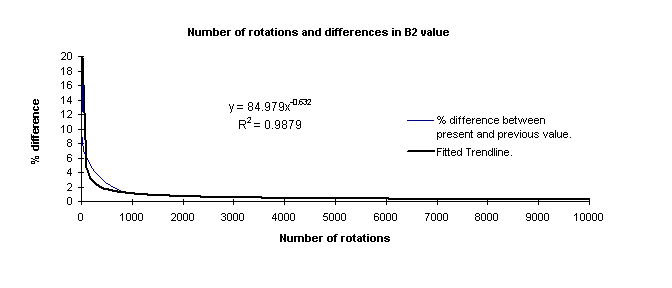
The exponential equation obtained was used to calculate a rough estimate of the
number of rotations required inorder to achieve a certain amount of accuracy. It is
found that if a % difference between the current and previous value of 0.001% is desired, it
would require approximately 63 million rotations -definitely takes too much
computing time. A difference of 0.01 percent requires about 1.65 million rotations.
Since the program allows four different values of number of rotations, the values
at smaller separation distances are set to be significantly greater that those at
further separations. In any way, the accuracy is inversely proportional to the
computation time. And gaining one requires a sacrifice of the other.
Back to the top.
Back to front page.



